-
Giải bài (AI)
-
Hỏi đáp
-
Giải bài tập SGK
- Lớp 2
- Tự nhiên và xã hội
- Tiếng việt
- Toán học
- Tiếng Anh
- Đạo đức
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 4
- Khoa học
- Tiếng việt
- Toán học
- Đạo đức
- Tiếng Anh
- Lịch sử và Địa lí
- Công nghệ
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 5
- Khoa học
- Toán học
- Tiếng việt
- Tin học
- Tiếng Anh
- Đạo đức
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- Lớp 6
- Công nghệ
- Tin học
- Lịch sử và Địa lí
- GDCD
- Ngữ văn
- Toán học
- Khoa học tự nhiên
- Tiếng Anh
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 7
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Lịch sử và Địa lí
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Âm nhạc
- Lớp 8
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Ngữ văn
- Khoa học tự nhiên
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 9
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Lịch sử và Địa lí
- Lớp 10
- Hóa học
- Tiếng Anh
- Lịch sử
- Sinh học
- Địa lí
- Vật lí
- Tin học
- Toán học
- GD kinh tế và pháp luật
- Công nghệ
- Ngữ văn
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- GD Quốc phòng và An ninh
- Lớp 11
- Hóa học
- Tiếng Anh
- Vật lí
- Tin học
- Toán học
- Địa lí
- Công nghệ
- Lịch sử
- Ngữ văn
- Sinh học
- GD Thể chất
- GD Quốc phòng và An ninh
- GD kinh tế và pháp luật
- HĐ trải nghiệm, hướng nghiệp
-
Trò chuyện
-
Chơi game

- KHÁM PHÁ
-
Giải bài (AI)
-
Hỏi đáp
-
Giải bài tập SGK
-
Tài liệu & đề thi
-
Ngữ pháp
-
Trò chuyện
- Tin tức học tập
- Chơi game
- FAVORITES
- Bảng tin
- Hỏi đáp
- Toán Học
- Lớp 9
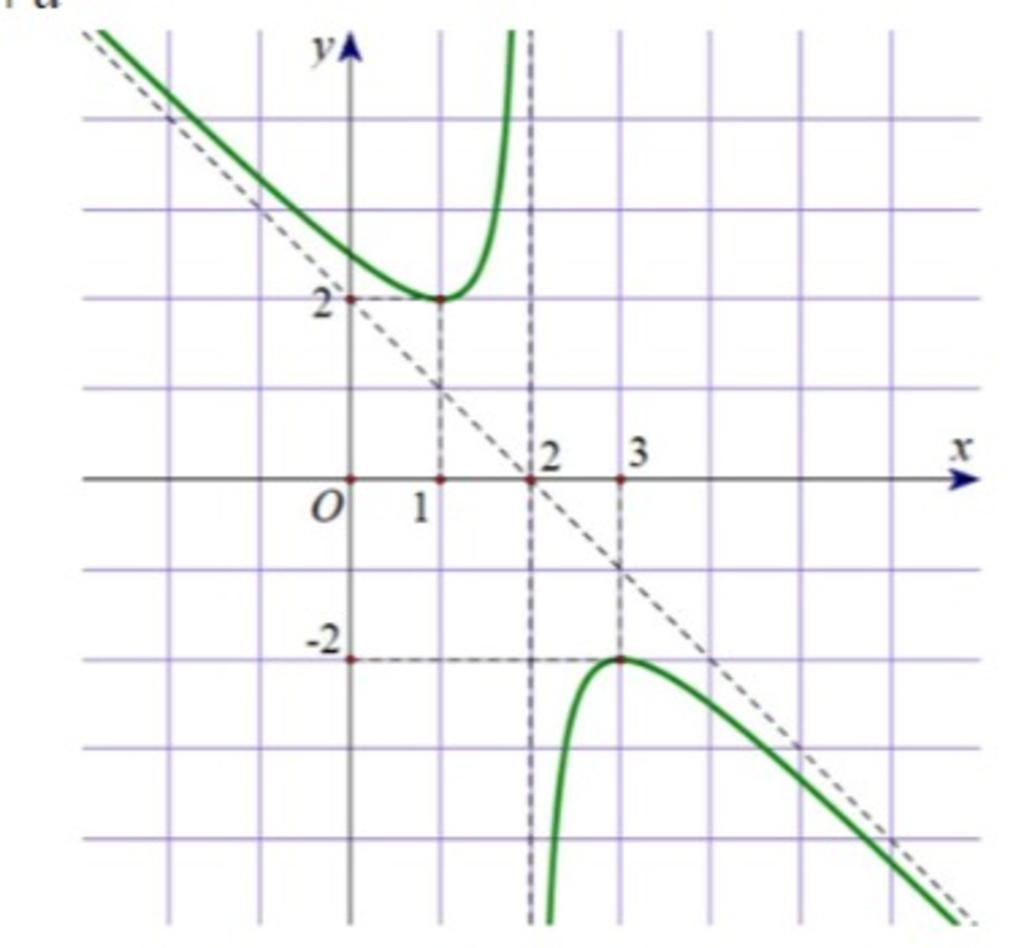
- Cho hàm số `y` `=` $dfrac{ax^2+bx+c}{x+d}$ có đồ thị như hình vẽ. `->` Khi đó, `a+b+c` `=` bao nhiêu
Cho hàm số `y` `=` $dfrac{ax^2+bx+c}{x+d}$ có đồ thị như hình vẽ. `->` Khi đó, `a+b+c` `=` bao nhiêu
Cho hàm số `y` `=` $\dfrac{ax^2+bx+c}{x+d}$ có đồ thị như hình vẽ.
`->` Khi đó, `a+b+c` `=` bao nhiêu?
Câu trả lời này dùng AI, hãy kiểm tra lại trước khi sử dụng
Hàm số được cho là: \( y = \frac{ax^2 + bx + c}{x + d} \).
Để xác định \( a + b + c \), chúng ta cần phân tích đồ thị của hàm số. Nhìn vào đồ thị:
1. Vị trí Tiệm cận đứng: Đồ thị có một tiệm cận đứng tại \( x = -d \). Quan sát đồ thị, ta thấy tiệm cận đứng này xảy ra khoảng \( x = -2 \), do đó \( d = 2 \).
2. Hệ số a: Đồ thị cho thấy hàm số có hai nhánh, một nhánh lên và một nhánh xuống. Để hàm số có dạng như vậy, \( a \) phải là âm, tức là \( a < 0 \).
3. Điểm cực trị: Nhìn vào đồ thị, có thể thấy là tại \( x = 2 \), hàm số có giá trị cực tiểu. Ở điểm này, giá trị của \( y(x) \) là gần \( y = -2 \) (theo đồ thị).
4. Giá trị của hàm tại điểm: Nếu thay \( x = 2 \) vào hàm số, ta được:
\[
y(2) = \frac{a(2^2) + b(2) + c}{2 + d} = -2
\]
Thay \( d = 2 \):
\[
\frac{4a + 2b + c}{4} = -2 \implies 4a + 2b + c = -8
\quad \text{(1)}
\]
5. Phân tích thêm điểm giao với trục Hoành: Đồ thị giao trục Hoành tại \( x = 0 \) và \( x = 4 \). Do đó:
Từ \( y(0) = 0 \):
\[
\frac{c}{d} = 0 \implies c = 0
\]
Từ \( y(4) = 0 \):
\[
\frac{a(4^2) + b(4) + c}{4 + d} = 0 \implies 16a + 4b + 0 = 0 \implies 16a + 4b = 0 \implies 4a + b = 0 \quad \text{(2)}
\]
6. Giải hệ phương trình: Từ phương trình (2), ta có:
\[
b = -4a
\]
Thay vào phương trình (1):
\[
4a + 2(-4a) + 0 = -8 \implies 4a - 8a = -8 \implies -4a = -8 \implies a = 2
\]
Do \( a < 0 \), chúng ta cần \( a = -2 \), rồi \( b = -4(-2) = 8 \) và \( c = 0 \).
7. Kết quả cuối cùng:
Tính \( a + b + c \):
\[
a + b + c = -2 + 8 + 0 = 6
\]
Vậy \( a + b + c = 6 \).
Để xác định \( a + b + c \), chúng ta cần phân tích đồ thị của hàm số. Nhìn vào đồ thị:
1. Vị trí Tiệm cận đứng: Đồ thị có một tiệm cận đứng tại \( x = -d \). Quan sát đồ thị, ta thấy tiệm cận đứng này xảy ra khoảng \( x = -2 \), do đó \( d = 2 \).
2. Hệ số a: Đồ thị cho thấy hàm số có hai nhánh, một nhánh lên và một nhánh xuống. Để hàm số có dạng như vậy, \( a \) phải là âm, tức là \( a < 0 \).
3. Điểm cực trị: Nhìn vào đồ thị, có thể thấy là tại \( x = 2 \), hàm số có giá trị cực tiểu. Ở điểm này, giá trị của \( y(x) \) là gần \( y = -2 \) (theo đồ thị).
4. Giá trị của hàm tại điểm: Nếu thay \( x = 2 \) vào hàm số, ta được:
\[
y(2) = \frac{a(2^2) + b(2) + c}{2 + d} = -2
\]
Thay \( d = 2 \):
\[
\frac{4a + 2b + c}{4} = -2 \implies 4a + 2b + c = -8
\quad \text{(1)}
\]
5. Phân tích thêm điểm giao với trục Hoành: Đồ thị giao trục Hoành tại \( x = 0 \) và \( x = 4 \). Do đó:
Từ \( y(0) = 0 \):
\[
\frac{c}{d} = 0 \implies c = 0
\]
Từ \( y(4) = 0 \):
\[
\frac{a(4^2) + b(4) + c}{4 + d} = 0 \implies 16a + 4b + 0 = 0 \implies 16a + 4b = 0 \implies 4a + b = 0 \quad \text{(2)}
\]
6. Giải hệ phương trình: Từ phương trình (2), ta có:
\[
b = -4a
\]
Thay vào phương trình (1):
\[
4a + 2(-4a) + 0 = -8 \implies 4a - 8a = -8 \implies -4a = -8 \implies a = 2
\]
Do \( a < 0 \), chúng ta cần \( a = -2 \), rồi \( b = -4(-2) = 8 \) và \( c = 0 \).
7. Kết quả cuối cùng:
Tính \( a + b + c \):
\[
a + b + c = -2 + 8 + 0 = 6
\]
Vậy \( a + b + c = 6 \).
Đăng phản hồi
© 2025 Học Tốt Online - Chia Sẻ Tài Liệu Học Tập và Giải Bài Tập Miễn Phí  Vietnamese
Vietnamese