Đề bài
Tìm tập hợp các giá trị nguyên của x sao cho \(P\left( x \right) = \frac{2}{{x + 1}}\) có giá trị là số nguyên.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức giá trị của phân thức tại một giá trị đã cho của biến để tính giá trị phân thức: Muốn tính giá trị của một phân thức tại một giá trị đã cho của biến ta thay giá trị đã cho của biến vào phân thức đó rồi tính giá trị biểu thức số nhận được.
+ Một phân số là số nguyên khi tử số chia hết cho mẫu số (hay mẫu số là ước của tử số).
Lời giải chi tiết
Điều kiện xác định \(x \ne - 1\)
Để P(x) có giá trị là một số nguyên thì \(\left( {x + 1} \right) \in \) Ư(2)\( = \left\{ {1; - 1;2; - 2} \right\}\).
Ta có bảng:
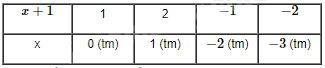
Vậy \(x \in \left\{ {0;\;1;\; - 2;\; - 3} \right\}\)
English
French
Spanish
Russian