Cặp số \(\left( {x;y} \right)\) nào dưới đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x - 5y = - 8\\4x + 3y = - 1\end{array} \right.\):
- A
\(\left( { - 1;1} \right)\)
- B
\(\left( { - 1; - 1} \right)\)
- C
\(\left( {1; - 1} \right)\)
- D
\(\left( {1;1} \right)\)
Đáp án : A
Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số
Với phương pháp cộng đại số:
+ Nhân hai vế của phương trình trên với \(4\) và nhân hai vế của phương trình dưới với \(3\) rồi trừ vế với vế của hai phương trình thu được.
+ Giải phương trình mới ta tìm được \(y\), thay vào phương trình còn lại ta tìm được \(x.\)
\(\left\{ \begin{array}{l}3x - 5y = - 8\\4x + 3y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12x - 20y = - 32\\12x + 9y = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12x - 20y - \left( {12x + 9y} \right) = - 32 - \left( { - 3} \right)\\12x + 9y = - 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 29y = - 29\\12x + 9y = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\12x + 9.1 = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\12x = - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = - 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( { - 1;1} \right)\)
Cho đoạn thẳng \(AB = 10cm\), \(M\) là trung điểm của \(AB\). Quỹ tích các điểm \(C\) trong mặt phẳng thỏa mãn tam giác \(ABC\) có \(C{A^2} + C{B^2} = 100\) là:
- A
Nửa đường tròn đường kính \(AB\)
- B
Đường tròn tâm \(M\) bán kính \(10cm\)
- C
Đường tròn tâm \(M\) bán kính \(5cm\)
- D
Đường tròn tâm \(M\) đường kính \(5cm\)
Đáp án : C
Sử dụng: “Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\). »
Vì \(C{A^2} + C{B^2} = 100 = A{B^2}\) nên \(\Delta ABC\) là tam giác vuông tại \(C\) hay điểm \(C\) luôn nhìn đoạn \(AB\) một góc \({90^0}\).
Do đó quỹ tích các điểm \(C\) là đường tròn đường kính \(AB = 10cm\) hay đường tròn tâm \(M\) bán kính \(5cm\).
Cho đường thẳng $d:y = x - 1$. Khi đó khoảng cách từ gốc tọa độ đến đường thẳng đã cho là:
- A
$2$
- B
$\sqrt 2 $
- C
$\dfrac{{\sqrt 2 }}{2}$
- D
\(\dfrac{{\sqrt 3 }}{2}\)
Đáp án : C
- Tìm giao điểm của đường thẳng với trục hoành, trục tung
- Dựng hình chiếu của tam giác được tạo thành
- Áp dụng hệ thức trong tam giác vuông để tính khoảng cách từ điểm $O$ đến $1$ đường thẳng.
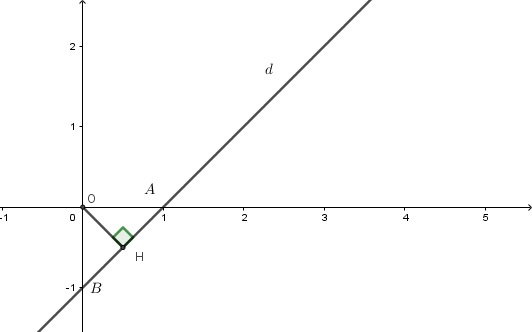
Ta có:
$d \cap Ox$ tại $A(1;0) \Rightarrow OA = 1$
$d \cap Oy $ tại $ B(0; - 1) \Rightarrow OB = 1$
Ta có $OA \bot OB$. Gọi $H$ là hình chiếu của $O$ trên đường thẳng $AB$.
Áp dụng hệ thức trong tam giác ta có:
$\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{1} + \dfrac{1}{1} = 2\\ \Rightarrow OH = \dfrac{{\sqrt 2 }}{2}\end{array}$
Đường thẳng nào sau đây đi qua điểm \(N\left( {1;1} \right)\)?
- A
\(2x + y - 3 = 0\)
- B
\(y - 3 = 0\)
- C
\(4x + 2y = 0\)
- D
\(5x + 3y - 1 = 0\)
Đáp án : A
Lần lượt thay tọa độ điểm \(N\) vào các phương trình đường thẳng. Phương trình nào được thỏa mãn thì đường thẳng đó đi qua \(N\).
+) Thay \(x = 1;y = 1\) vào \(2x + y - 3 = 0\) ta được \(2.1 + 1 - 3 = 0\) nên điểm \(N\) thuộc đường thẳng \(2x + y - 3 = 0\)
+) Thay \(x = 1;y = 1\) vào \(y - 3 = 0\) ta được \(1 - 3 = - 2 \ne 0\)
+) Thay \(x = 1;y = 1\) vào \(4x + 2y = 0\) ta được \(4.1 + 2.1 = 6 \ne 0\)
+) Thay \(x = 1;y = 1\) vào \(5x + 3y - 1 = 0\) ta được \(5.1 + 3.1 - 1 = 7 \ne 0\)
Vậy đường thẳng \(d:2x + y - 3 = 0\) đi qua \(N\left( {1;1} \right)\).
Hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) có các hệ số khác 0 và \(\dfrac{a}{{a'}} = \dfrac{b}{{b'}} \ne \dfrac{c}{{c'}}\). Chọn câu đúng.
- A
Hệ phương trình có nghiệm duy nhất
- B
Hệ phương trình vô nghiệm
- C
Hệ phương trình vô số nghiệm
- D
Chưa kết luận được về nghiệm của hệ
Đáp án : B
Xét hệ phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (các hệ số \(a';b';c'\)khác 0)
Hệ phương trình vô nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} \ne \dfrac{c}{{c'}}\)
Hai bạn A và B đi xe máy khởi hành từ $2$ địa điểm cách nhau $210{\rm{ }}km,$ đi ngược chiều nhau và gặp nhau sau $3h.$ Tìm vận tốc của mỗi người biết nếu $A$ tăng vận tốc thêm $5{\rm{ }}km/h$ và B giảm vận tốc $5km/h$ thì vận tốc của $A$ bằng vận tốc của $B.$
- A
$40km/h$ và $30km/h$
- B
$40km/h$ và$45km/h$
- C
$30km/h$ và $40km/h$
- D
$45km/h$ và$30km/h$
Đáp án : C
Các bước giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình
1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)
2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết
3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải hệ phương trình
Sử dụng các phương pháp thế, cộng đại số, đặt ẩn phụ…
Bước 3: Kết luận
Gọi vận tốc của $A$ và $B$ lần lượt là $x,{\rm{ }}y{\rm{ }}\left( {km/h;{\rm{ }}x,{\rm{ }}y > 0} \right)$
Hai người đi ngược chiều và gặp nhau sau $3h$ nên ta có phương trình : $3x + 3y = 210\,\,(1)$
Nếu A tăng vận tốc thêm $5{\rm{ }}km/h$ và $B$ giảm vận tốc $5km/h$ thì vận tốc của $A$ bằng vận tốc của $B$ nên ta có phương trình: $x + 5 = y - 5\,\,\,\,(2)$
Từ (1) và (2) ta có hệ phương trình:
$\left\{ \begin{array}{l}3x + 3y = 210\\x + 5 = y - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 70\\x - y = - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 60\\x + y = 70\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 30\\y = 40\end{array} \right.(tmdk)$
Vậy vận tốc của A và B lần lượt là $30km/h$ và $40km/h.$
Cho $2$ đường thẳng $d:y = 2x - 1;d':y = (m - 3)x + 2$. Tìm $m$ để $d$ cắt $d'$ mà hoành độ và tung độ giao điểm cùng dấu.
- A
$\left\{ \begin{array}{l}m < 1\\m \ne - 5\end{array} \right.$
- B
$\left\{ \begin{array}{l}m > - 1\\m \ne 5\end{array} \right.$
- C
$\left\{ \begin{array}{l}m < 5\\m > 1\end{array} \right.$
- D
$m>-1$
Đáp án : B
- Tìm tọa độ giao điểm 2 đường thẳng cho trước
- Hoành độ và tung độ giao điểm cùng dấu $ \Leftrightarrow xy > 0$.
Ta có $d \cap d' \Leftrightarrow m - 3 \ne 2 \Leftrightarrow m \ne 5$.
Xét phương trình hoành độ của $d'$ và $d''$ :
$\begin{array}{l}2x - 1 = (m - 3)x + 2 \Leftrightarrow (m - 5)x = - 3 \Leftrightarrow x = \dfrac{{ - 3}}{{m - 5}}\\ \Rightarrow y = \dfrac{{ - 6}}{{m - 5}} - 1 = \dfrac{{ - m - 1}}{{m - 5}}\end{array}$
Theo đề bài: $x.y > 0 \Leftrightarrow \dfrac{{ - 3}}{{m - 5}}.\dfrac{{ - m - 1}}{{m - 5}} > 0 \Leftrightarrow \dfrac{{3(m + 1)}}{{{{(m - 5)}^2}}} > 0$
Mà ${(m - 5)^2} > 0,\forall m \ne 5$
Suy ra $m > - 1$
Kết hợp điều kiện ta có: $\left\{ \begin{array}{l}m > - 1\\m \ne 5\end{array} \right.$.
Thu gọn biểu thức \(\sqrt[3]{{{x^3} - 3{x^2} + 3x - 1}} - \sqrt[3]{{125{x^3} + 75{x^2} + 15x + 1}}\) ta được:
- A
\( - 4x-2\)
- B
\( - 6x\)
- C
\(-4x\)
- D
\(4x+2\)
Đáp án : A
- Đưa biểu thức dưới dấu căn về hằng đẳng thức \({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)
- Áp dụng \(\sqrt[3]{{{a^3}}} = a\)
Ta có: \(\sqrt[3]{{{x^3} - 3{x^2} + 3x - 1}} - \sqrt[3]{{125{x^3} + 75{x^2} + 15x + 1}}\)\( = \sqrt[3]{{{{\left( {x - 1} \right)}^3}}} - \sqrt[3]{{{{\left( {5x + 1} \right)}^3}}}\)
\( = x - 1 - 5x - 1 = - 4x-2.\)
Chọn câu sai.
- A
Thể tích hình nón có chiều cao \(h\) và bán kính đáy \(R\) là \(V = \dfrac{1}{3}\pi {R^2}h\)
- B
Thể tích khối cầu có bán kính \(R\) là \(V = \pi {R^3}\)
- C
Diện tích hình cầu có bán kính \(R\) là \(S = 4\pi {R^2}\)
- D
Đường sinh của hình nón có chiều cao \(h\) và bán kính đáy \(R\) là \(l = \sqrt {{R^2} + {h^2}} \)
Đáp án : B
Áp dụng các công thức liên quan đến hình nón và hình cầu
Ta có
+ Thể tích hình nón có chiều cao \(h\) và bán kính đáy \(R\) là \(V = \dfrac{1}{3}\pi {R^2}h\) nên A đúng
+ Diện tích hình cầu có bán kính \(R\) là \(S = 4\pi {R^2}\) nên C đúng
+ Đường sinh của hình nón có chiều cao \(h\) và bán kính đáy \(R\) là \(l = \sqrt {{R^2} + {h^2}} \) nên D đúng
+ Thể tích khối cầu có bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\) nên B sai.
Cho các hình vuông $ABCD$ có cạnh $AB$ cố định. Tìm quỹ tích giao điểm $O$ của hai đường chéo của các hình vuông đó.
- A
Quỹ tích điểm $O$ là $2$ cung chứa góc \({120^0}\) dựng trên $AB$ .
- B
Quỹ tích điểm $O$ là nửa đường tròn đường kính $AB$ , trừ hai điểm $A$ và$B$ .
- C
Quỹ tích điểm $O$ là $2$ cung chứa góc \({60^0}\) dựng trên $AB$ .
- D
Quỹ tích điểm $O$ là $2$ cung chứa góc \({30^0}\) dựng trên $AB$ .
Đáp án : B
Sử dụng phương pháp cung chứa góc.
Hai điểm $B,C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là $2$ cung chứa góc \(\alpha \) dựng trên $BC$ .

Xét hình vuông $ABCD$ có hai đường chéo $AC$ và $BD$ vuông góc với nhau tại trung điểm của mỗi đường.
Suy ra \(AO \bot BO \Rightarrow \) \(\widehat {AOB} = {90^\circ }\)
Ta có \(\widehat {AOB} = {90^0}\) không đổi mà $A,B$ cố định
\( \Rightarrow \) Quỹ tích điểm $O$ là nửa đường tròn đường kính $AB$ trừ hai điểm $A$ và $B.$
Số nghiệm của hệ phương trình sau: \(\left\{ \begin{array}{l}\left| x \right| + 4\left| y \right| = 18\\3\left| x \right| + \left| y \right| = 10\end{array} \right.\) là:
- A
2
- B
4
- C
3
- D
1
Đáp án : B
+ Đặt: \(\left| x \right| = a \ge 0;\,\,\,\left| y \right| = b \ge 0\).
+ Giải hệ phương trình ẩn \(a;b\) bằng phương pháp thế hoặc cộng đại số.
+ Thay trở lại cách đặt ta tìm được \(x;y.\)
Đặt: \(\left| x \right| = a \ge 0;\,\,\left| y \right| = b \ge 0\).
Khi đó, ta có hệ phương trình: \( \Leftrightarrow \left\{ \begin{array}{l}a + 4b = 18\\3a + b = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 18 - 4b\\3\left( {18 - 4b} \right) + b = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 18 - 4b\\b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\end{array} \right.\,\,\left( {tm} \right)\).
\( \Rightarrow \left\{ \begin{array}{l}\left| x \right| = 2\\\left| y \right| = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \pm 2\\y = \pm 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 2\\y = 4\end{array} \right.\\\left\{ \begin{array}{l}x = - 2\\y = 4\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = - 4\end{array} \right.\\\left\{ \begin{array}{l}x = - 2\\y = - 4\end{array} \right.\end{array} \right.\)
Cho \(A = 3\sqrt[3]{2}\) và \(B = \sqrt[3]{{42}}\). Chọn khẳng định đúng.
- A
\(A < B\)
- B
\(A > B\)
- C
\(A \ge B\)
- D
\(A + B = 0\)
Đáp án : B
- Sử dụng công thức \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).
- So sánh hai căn bậc hai theo \(a < b \Leftrightarrow \sqrt[3]{a} < \sqrt[3]{b}\).
Ta có: \(A = 3\sqrt[3]{2} = \sqrt[3]{{27}}.\sqrt[3]{2} = \sqrt[3]{{54}}\).
Vì \(54 > 42 \) nên \( \sqrt[3]{{54}} > \sqrt[3]{{42}} \Rightarrow 3\sqrt[3]{2} > \sqrt[3]{{42}}\) hay \(A > B\).
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right).\) Biết \(\widehat {BOD} = {130^0}\) thì số đo \(\widehat {BAD}\) là:
- A
\({50^0}\)
- B
\({130^0}\)
- C
\({15^0}\)
- D
\({65^0}\)
Đáp án : D
Sử dụng góc nội tiếp bằng một nửa số đo của cung bị chắn, số đo góc ở tâm bằng số đo cung bị chắn.

Ta có: \(\widehat {BOD} = {130^0} \Rightarrow sđ\,\overparen{BD} = {130^0}\).
Do đó \(\widehat {BAD} = \dfrac{1}{2}sđ\overparen{BD} = {65^0}\) (góc nội tiếp bằng một nửa số đo của cung bị chắn)
Trên một cánh đồng cấy $50$ ha lúa giống mới và $30$ ha lúa giống cũ, thu hoạch được tất cả $410$ tấn thóc. Hỏi năng suất lúa cũ trên $1$ ha là bao nhiêu, biết rằng $5$ ha trồng lúa mới thu hoạch được nhiều hơn $6$ ha trồng lúa cũ là $0,5$ tấn.
- A
$5,5$ tấn
- B
$4$ tấn
- C
$4,5$ tấn
- D
$3$ tấn
Đáp án : C
Gọi năng suất lúa mới và lúa cũ trên $1$ ha lần lượt là $x;y\,\,\left( {x,y > 0} \right),$ đơn vị: tấn/ha
Lập hệ phương trình theo x, y và giải hệ đó.
Gọi năng suất lúa mới và lúa cũ trên $1$ ha lần lượt là $x;y\,\,\left( {x,y > 0} \right),$ đơn vị: tấn/ha
Vì cấy $50$ ha lúa giống mới và $30$ ha lúa giống cũ, thu hoạch được tất cả $410$ tấn thóc nên ta có
$50x + 30y = 410$
Vì $5$ ha trồng lúa mới thu hoạch được nhiều hơn $6$ ha trồng lúa cũ là $0,5$ tấn nên ta có phương trình
$5x - 6y = 0,5$
Suy ra hệ phương trình $\left\{ \begin{array}{l}5x - 6y = 0,5\\50x + 30y = 410\end{array} \right. $
Nhân cả hai vế của phương trình thứ hai với \(\frac{1}{10}\), ta được:
$\left\{ \begin{array}{l}5x - 6y = 0,5\\5x + 3y = 41\end{array} \right.$
Trừ hai vế của phương trình thứ hai cho phương trình thứ nhất, ta được: $9y = 40,5$ suy ra $y = 4,5(tm)$
Thay vào $5x - 6y = 0,5$ ta tính được $x = 5,5(tm)$
Vậy năng suất lúa cũ trên $1$ ha là $4,5$ tấn.
Phương trình \(\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}\) có bao nhiêu nghiệm?
- A
\(1\)
- B
\(0\)
- C
\(2\)
- D
\(3\)
Đáp án : B
Giải phương trình dạng \(\sqrt A = \sqrt B \)
ĐK: \(A \ge 0\) (hoặc \(B \ge 0\) )
Khi đó \(\sqrt A = \sqrt B \Leftrightarrow A = B\)
So sánh với điều kiện rồi kết luận.
Điều kiện: \(x \ge 5\)
Ta có \(\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}\)\( \Leftrightarrow x - 5 = 3 - x \Leftrightarrow x + x = 3 + 5 \Leftrightarrow 2x = 8 \Leftrightarrow x = 4\,\,\left( {KTM} \right)\)
Vậy phương trình đã cho vô nghiệm.
Tìm hệ số góc của đường thẳng \(d:y = \left( {2m + 5} \right)x + 1\) biết nó vuông góc với đường thẳng \(d':y - 2x = 0\).
- A
\( - 2\)
- B
\( - \dfrac{1}{2}\)
- C
\(\dfrac{1}{2}\)
- D
\(2\)
Đáp án : B
+ Sử dụng điều kiện vuông góc của hai đường thẳng để tìm \(m\).
+ Sau đó sử dụng lý thuyết về hệ số góc để tìm hệ số góc của đường thẳng \(d'\)
Đường thẳng có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) có \(a\) là hệ số góc.
Ta có \(d':y - 2x = 0\)\( \Leftrightarrow y = 2x\)
Đường thẳng \(d:y = \left( {2m + 5} \right)x + 1\) có hệ số góc \(2m + 5\)
Vì \(d \bot d' \Rightarrow \left( {2m + 5} \right).2 = - 1 \Leftrightarrow 2m + 5 = - \dfrac{1}{2}\)
Suy ra đường thẳng \(d:y = \left( {2m + 5} \right)x + 1\) có hệ số góc \(k = - \dfrac{1}{2}\)
Cho \(\tan a = 3.\) Khi đó \(\cot a\) bằng
- A
\(\dfrac{1}{3}\)
- B
\(3\)
- C
\(\sqrt 3 \)
- D
\(\dfrac{1}{2}\)
Đáp án : A
Sử dụng \(\tan a.\cot a = 1\) để tìm \(\cot a.\)
Ta có \(\tan a.\cot a = 1\) nên \(\cot a = \dfrac{1}{{\tan a}} = \dfrac{1}{3}.\)
Cho hệ phương trình \(\left\{ \begin{array}{l}5x\sqrt 3 + y = 2\sqrt 2 \\x\sqrt 6 - y\sqrt 2 = 2\end{array} \right.\). Biết nghiệm của hệ phương trình là $\left( {x;y} \right)$, tính $6x + 3\sqrt 3 y$
- A
$\dfrac{{\sqrt 6 }}{2}$
- B
$\dfrac{{5\sqrt 6 }}{2}$
- C
$ - \dfrac{{\sqrt 6 }}{2}$
- D
$\sqrt 6 $
Đáp án : C
Giải hệ phương trình bằng phương pháp cộng đại số
Nhân hai vế của phương trình thứ nhất với \(\sqrt 2 \) rồi cộng từng vế của hai phương trình
\(\left\{ \begin{array}{l}5x\sqrt 3 + y = 2\sqrt 2 \\x\sqrt 6 - y\sqrt 2 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x\sqrt 6 + y\sqrt 2 = 4\\x\sqrt 6 - y\sqrt 2 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x\sqrt 6 = 6\\x\sqrt 6 - y\sqrt 2 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{{\sqrt 6 }}\\\dfrac{1}{{\sqrt 6 }}.\sqrt 6 - y\sqrt 2 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{{\sqrt 6 }}\\1 - y\sqrt 2 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{{\sqrt 6 }}\\y\sqrt 2 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{\sqrt 6 }}{6}\\y = - \dfrac{{\sqrt 2 }}{2}\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {\dfrac{{\sqrt 6 }}{6}; - \dfrac{{\sqrt 2 }}{2}} \right)\)
$ \Rightarrow 6x + 3\sqrt 3 y = 6.\dfrac{{\sqrt 6 }}{6} + 3\sqrt 3 .\left( { - \dfrac{{\sqrt 2 }}{2}} \right) = \sqrt 6 - \dfrac{3}{2}\sqrt 6 = - \dfrac{{\sqrt 6 }}{2}.$
Kết quả của phép tính \(\left( {\sqrt {28} - 2\sqrt 3 + \sqrt 7 } \right)\sqrt 7 + \sqrt {84} \) là
- A
\(7\)
- B
\(7 + 2\sqrt {21} \)
- C
\(7 + \sqrt {21} \)
- D
\(21\)
Đáp án : D
Sử dụng công thức
+ Khai phương một tích: \(\sqrt {A.B} = \sqrt A .\sqrt B {\rm{ }}\,(A \ge 0,B \ge 0)\)
Ta có \(\left( {\sqrt {28} - 2\sqrt 3 + \sqrt 7 } \right)\sqrt 7 + \sqrt {84} \)\( = \left( {\sqrt {4.7} - 2\sqrt 3 + \sqrt 7 } \right).\sqrt 7 + \sqrt {4.21} \)
\( = \left( {2\sqrt 7 - 2\sqrt 3 + \sqrt 7 } \right).\sqrt 7 + 2\sqrt {21} = \left( {3\sqrt 7 - 2\sqrt 3 } \right).\sqrt 7 + 2\sqrt {21} \)
\( = 3\sqrt 7 .\sqrt 7 - 2\sqrt 3 .\sqrt 7 + 2\sqrt {21} \) \( = 21 - 2\sqrt {21} + 2\sqrt {21} = 21\)
Cho parabol\((P):y = 5{x^2}\) và đường thẳng \((d):y = - 4x - 4\). Số giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là:
- A
\(1\)
- B
\(0\)
- C
\(3\)
- D
\(2\)
Đáp án : B
Cho parabol \((P):y = {\rm{a}}{{\rm{x}}^2}(a \ne 0)\) và đường thẳng \(d:y = mx + n\). Để tìm tọa độ giao điểm (nếu có) của \((d)\) và \((P)\), ta làm như sau:
Bước 1. Xét phương trình hoành độ giao điểm của \((d)\) và \((P)\) :\({\rm{a}}{{\rm{x}}^2} = mx + n\)
Bước 2. Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó suy ra số giao điểm của parabol và đường thẳng
Xét phương trình hoành độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \((d):\)
\(5{x^2} = - 4x - 4 \Leftrightarrow 5{x^2} + 4x + 4 = 0 \\\Leftrightarrow {x^2} + 4{x^2} + 4x + 4 = 0 \\\Leftrightarrow {x^2} + {\left( {x + 2} \right)^2} = 0\,\,\left( * \right)\)
Xét \({x^2} + {\left( {x + 2} \right)^2} \ge 0;\forall x\) và dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\) (vô lý) nên \({x^2} + {\left( {x + 2} \right)^2} > 0;\forall x\)
Hay phương trình (*) vô nghiệm.
Vậy không có giao điểm của đường thẳng \((d)\) và parabol \(\left( P \right)\).
Tính giá trị của \(x\) trên hình vẽ

- A
\(2\sqrt 6 \)
- B
\(\sqrt 6 \)
- C
\(3\sqrt 6 \)
- D
\(27\)
Đáp án : C
Sử dụng hệ thức lượng trong tam giác vuông: “ Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông lên cạnh huyền”
Xét tam giác \(MNP\) vuông tại \(M,\) có \(MK \bot NP\) ta có \(M{K^2} = NK.PK\) (hệ thức lượng trong tam giác vuông)
Hay \({x^2} = 6.9 \Leftrightarrow {x^2} = 54 \Rightarrow x = 3\sqrt 6 \,.\)
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {130^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), kẻ \(Bx \bot BA;Cy \bot CA\), \(Bx\) và \(Cy\) cắt nhau tại D. Chọn đáp án sai.
- A
\(\Delta BCD\) cân
- B
\(ABDC\) nội tiếp
- C
\(ABDC\) là hình thoi
- D
\(\widehat {BDC} = 50^\circ \)
Đáp án : C
Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.

Theo đề bài ta có \(\widehat {ABD} = \widehat {ACD} = 90^\circ \Rightarrow \widehat {ABD} + \widehat {ACD} = 90^\circ + 90^\circ = 180^\circ \) mà hai góc \(\widehat {ABD};\widehat {ACD}\) ở vị trí đối nhau nên tứ giác \(ABDC\) là tứ giác nội tiếp nên đáp án B đúng.
+ Lại có \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = 130^\circ \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac{{180^\circ - 130^\circ }}{2} = 25^\circ \)
+ Ta có \(\widehat {BDC} + \widehat {ABC} = 90^\circ \Rightarrow \widehat {BDC} = 90^\circ - 25^\circ = 65^\circ \)
Và \(\widehat {BCD} + \widehat {ACB} = 90^\circ \Rightarrow \widehat {BCD} = 90^\circ - 25^\circ = 65^\circ \)
Từ đó suy ra tam giác \(BCD\) cân tại \(D\) nên đáp án A đúng.
+ Xét tứ giác \(ABDC\) nội tiếp nên \(\widehat {BAC} + \widehat {BDC} = 180^\circ \Leftrightarrow \widehat {BDC} = 180^\circ - \widehat {BAC} = 180^\circ - 130^\circ = 50^\circ \) nên D đúng.
Ta chưa đủ điều kiện để suy ra tứ giác \(ABDC\) là hình thoi nên C sai.
Cho \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\) và \(C = \left( {2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} } \right):\sqrt 3 \). Chọn đáp án đúng.
- A
\(B > C\)
- B
\(B < C\)
- C
\(B = C\)
- D
\(B = - C\)
Đáp án : A
+ Tính \(B;C\) bằng cách sử dụng các công thức
Với \(A > 0\) và \(A \ne {B^2}\) thì \(\dfrac{C}{{\sqrt A \pm B}} = \dfrac{{C(\sqrt A \mp B)}}{{A - {B^2}}}\)
Khai phương một tích: \(\sqrt {A.B} = \sqrt A .\sqrt B {\rm{ }}(A \ge 0,B \ge 0)\)
+ So sánh \(B;C.\)
Ta có \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\)
\( = \dfrac{{2\sqrt 2 }}{{\sqrt 2 .\sqrt 2 }} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{\left( {\sqrt 3 - \sqrt 2 } \right)\left( {\sqrt 3 + \sqrt 2 } \right)}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}\)
$
= \dfrac{{2\sqrt 2 }}{2} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{3 - 2}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{3 - 1}}$
$= \sqrt 2 + \dfrac{{\sqrt 3 + \sqrt 2 }}{1} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{2}$
\( = \sqrt 2 + \sqrt 3 + \sqrt 2 - \left( {\sqrt 3 + 1} \right)\)
\( = \sqrt 2 + \sqrt 3 + \sqrt 2 - \sqrt 3 - 1\)
\( = 2\sqrt 2 - 1\)
Lại có
$\begin{array}{l}C = (2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} ):\sqrt 3 \\ = \left( {2\sqrt 3 - 5\sqrt {9.3} + 4\sqrt {4.3} } \right):\sqrt 3 \\= (2\sqrt 3 - 5.3\sqrt 3 + 4.2\sqrt 3 ):\sqrt 3 \\ = - 5\sqrt 3 :\sqrt 3 \\ = - 5\end{array}$
Nhận thấy \(B = 2\sqrt 2 - 1 > 0;\,C = - 5 < 0 \Rightarrow B > C\)
Phương trình \(\left( {\dfrac{{2 + x}}{{2 - x}} - \dfrac{{2 - x}}{{2 + x}}} \right):\left( {\dfrac{{2 + x}}{{2 - x}} + 1} \right) = \dfrac{2}{3x}\) có nghiệm là:
- A
\(x = - 1;x = \dfrac{2}{3}.\)
- B
\(x = 1;x = - \dfrac{2}{3}.\)
- C
\(x = 3\)
- D
\(x = - 1;x = - \dfrac{2}{3}.\)
Đáp án : B
Giải phương trình chứa ẩn ở mẫu số
Bước 1: Tìm điều kiện xác định của phương trình
Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức.
Bước 3: Giải phương trình vừa nhận được
Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thoả mãn điều kiện xác định, các giá trị thoả mãn điều kiện xác định là nghiệm của phương trình đã cho
Điều kiện: \(x \ne 2;x \ne - 2;x \ne 0\)
Ta có \(\left( {\dfrac{{2 + x}}{{2 - x}} - \dfrac{{2 - x}}{{2 + x}}} \right):\left( {\dfrac{{2 + x}}{{2 - x}} + 1} \right) = \dfrac{2}{{3x}}\)\( \Leftrightarrow \dfrac{{{{\left( {2 + x} \right)}^2} - {{\left( {2 - x} \right)}^2}}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}:\dfrac{{2 + x + 2 - x}}{{2 - x}} = \dfrac{2}{{3x}}\)
\( \Leftrightarrow \dfrac{{8x}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}.\dfrac{{2 - x}}{4} = \dfrac{2}{{3x}} \Leftrightarrow \dfrac{{2x}}{{2 + x}} = \dfrac{2}{{3x}}\)\( \Rightarrow 6{x^2} - 2x - 4 = 0 \Leftrightarrow 3{x^2} - x - 2 = 0\)
Phương trình này có \(a + b + c = 3 + \left( { - 1} \right) + \left( { - 2} \right) = 0\) nên có hai nghiệm phân biệt \(x = 1;x = \dfrac{{ - 2}}{3}\left( {TM} \right)\)
Vậy phương trình có hai nghiệm \(x = 1;x = - \dfrac{2}{3}.\)
Đồ thị hàm số $y = (3 - m)x + m + 3$ đi qua gốc tọa độ khi:
- A
$m = - 3$
- B
$m = 3$
- C
$m \ne 3$
- D
$m \ne \pm 3$
Đáp án : A
Sử dụng kiến thức: Điểm thuộc đồ thị hàm số.
Điểm $M(x_0;y_0)$ thuộc đồ thị hàm số $y=ax+b$ \( \Leftrightarrow {y_0} = a{x_0} + b\)
Ta có điểm $O\left( {0\;;0} \right)$ thuộc đường thẳng $y = (3 - m)x + m + 3 \Leftrightarrow (3-m).0+m + 3 = 0 $$\Leftrightarrow m+3=0\Leftrightarrow m = - 3$
Tính thể tích của một hình nón cụt có các bán kính đáy bằng \(4 cm\) và \(7cm\), chiều cao bằng \(11 cm.\)
- A
$1023\pi \,\,\left( {c{m^3}} \right)$
- B
$341\pi \,\,\left( {c{m^3}} \right)$
- C
$93\pi \,\,\left( {c{m^3}} \right)$
- D
$314\pi \,\,\left( {c{m^3}} \right)$
Đáp án : B
Sử dụng công thức tính thể tích hình nón cụt $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2})$ với các bán kính đáy là $R$ và $r,$chiều cao $h.$

Thể tích nón cụt là $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}) = \dfrac{1}{3}.\pi .11\left( {{4^2} + 4.7 + {7^2}} \right) = 341\pi \,\,\left( {c{m^3}} \right)$
Tìm điều kiện của $x$ để căn thức \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa.
- A
$x \ge 1$
- B
\(x < 1\)
- C
\(x > 1\)
- D
\(x = 1\)
Đáp án : C
\(\sqrt A \) xác định (hay có nghĩa) khi \(A\) lấy giá trị không âm tức là \(A \ge 0.\)
Ngoài ra: \(\dfrac{1}{A} \ge 0 \Leftrightarrow A > 0\)
Ta có \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa \( \Leftrightarrow \dfrac{1}{{x - 1}} \ge 0 \Rightarrow x - 1 > 0\) (vì $1>0$)
\( \Leftrightarrow x > 1\)
Cho hai vòi nước cùng lúc chảy vào một bể cạn. Nếu chảy riêng từng vòi thì vòi thứ nhất chảy đầy bể chậm hơn vòi thứ hai \(2\) giờ. Khi nước đầy bể, người ta khóa vòi thứ nhất và vòi thứ hai lại, đồng thời mở vòi thứ ba cho nước chảy ra thì sau \(7,5\) giờ bể cạn nước. Khi nước trong bể đã cạn mở cả ba vòi thì sau \(20\) giờ bể lại đầy nước. Hỏi nếu chỉ dùng vòi thứ nhất thì sau bao lâu bể đầy nước?
- A
\(9\) giờ
- B
\(12\) giờ
- C
\(10\) giờ
- D
\(8\) giờ
Đáp án : C
Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là \(x\) (giờ), \(\left( {x > 2} \right)\).
Trong một giờ:
-Vòi thứ nhất chảy được \(\dfrac{1}{x}\) ( bể).
- Vòi thứ hai chảy được \(\dfrac{1}{{x - 2}}\) ( bể).
- Vì vòi thứ ba chảy ra trong 7,5 giờ thì cạn bề nên trong 1h vòi thứ ba chảy được \(\dfrac{2}{{15}}\) ( bể).
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình \(\dfrac{1}{x} + \dfrac{1}{{x - 2}} - \dfrac{2}{{15}} = \dfrac{1}{{20}} \Leftrightarrow \dfrac{1}{x} + \dfrac{1}{{x - 2}} = \dfrac{{11}}{{60}}\) \( \Leftrightarrow \dfrac{{x - 2 + x}}{{x\left( {x - 2} \right)}} = \dfrac{{11}}{{60}} \Leftrightarrow \dfrac{{2x - 2}}{{{x^2} - 2x}} = \dfrac{{11}}{{60}}\)
\( \Rightarrow 120x - 120 = 11{x^2} - 22x\) \( \Leftrightarrow 11{x^2} - 142x + 120 = 0\) có \(\Delta ' = 3721 \Rightarrow \sqrt {\Delta '} = 61\) nên phương trình có hai nghiệm \(\left[ \begin{array}{l}x = \dfrac{{71 - 61}}{{11}} = \dfrac{{10}}{{11}}\left( {ktm} \right)\\x = \dfrac{{71 + 61}}{{11}} = 12\left( {tm} \right)\end{array} \right.\)
Vậy chỉ dùng vòi thứ nhất thì sau \(10\) giờ bể đầy nước.
Tập nghiệm của phương trình \(x + 4\sqrt x - 12 = 0\) là:
- A
\(S = \left\{ {36} \right\}\)
- B
\(S = \left\{ {4;\,\,36} \right\}\)
- C
\(S = \left\{ 4 \right\}\)
- D
\(S = \left\{ {2; - 6} \right\}\)
Đáp án : C
Đặt: \(\sqrt x = t\,\,\left( {t \ge 0} \right)\), khi đó đưa về được phương trình bậc hai: \({t^2} + 4t - 12 = 0\). Giải phương trình bậc hai ẩn \(t\) sau đó quay lại tìm được \(x\).
\(x + 4\sqrt x - 12 = 0\) (1)
ĐKXĐ: \(x \ge 0.\)
Đặt: \(\sqrt x = t\,\,\left( {t \ge 0} \right)\)
\(\left( 1 \right) \Leftrightarrow {t^2} + 4t - 12 = 0.\)
Có: \(\Delta ' = {2^2} + 12 = 16 > 0 \Rightarrow \) phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{t_1} = - 2 + \sqrt {16} = 2\,\,\,\left( {tm} \right)\\{t_2} = - 2 - \sqrt {16} = - 6\,\,\,\left( {ktm} \right)\end{array} \right..\)
Với \(t = 2 \Rightarrow \sqrt x = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right).\)
Vậy phương trình có nghiệm \(x = 4.\)
Một hình trụ có bán kính đáy bằng \(5\,cm\) và diện tích xung quanh bằng \(300\pi \,\left( {c{m^2}} \right)\) . Chiều cao của hình trụ là
- A
\(30\,cm\)
- B
$12\,cm$
- C
\(6\,cm\)
- D
\(10\,cm\)
Đáp án : A
Sử dụng công thức tính diện tích xung quanh hình trụ có bán kính đáy $R$ và chiều cao \(h\) là \({S_{xq}} = 2\pi {R}h\)
Gọi chiều cao của hình trụ là \(h.\) Ta có \({S_{xq}} = 2\pi R.h \Leftrightarrow 2\pi {.5}.h = 300\pi \Leftrightarrow h = 30\,cm.\)
Cho hình trụ có bán kính đáy \(R\) và chiều cao \(h\) . Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì
- A
Thể tích hình trụ không đổi
- B
Diện tích toàn phần không đổi
- C
Diện tích xung quanh không đổi
- D
Chu vi đáy không đổi
Đáp án : C
Sử dụng các công thức tính chu vi đáy, diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ (phần lý thuyết)
Chiều cao mới của hình trụ là \(h' = 2h\) ; bán kính đáy mới là \(R' = \dfrac{R}{2}\)
Hình trụ mới có :
Chu vi đáy \(2\pi R' = 2\pi \dfrac{R}{2} = \pi R < 2\pi R = C\) nên phương án D sai.
Diện tích toàn phần \(2\pi R'h + 2\pi {R'^2} = 2\pi Rh + \dfrac{{\pi {R^2}}}{2} \ne 2\pi Rh + 2\pi {R^2}\) nên phương án B sai.
Thể tích \(\pi {R'^2}h = \dfrac{{\pi {R^2}h}}{4} \ne \pi {R^2}h\) nên phương án A sai.
Diện tích xung quanh \(2\pi R'h = 2\pi .\dfrac{R}{2}.2h = 2\pi Rh\) nên phương án C đúng.
Một ca nô xuôi dòng trên một khúc sông từ A đến B dài 80 km, sau đó lại ngược dòng đến địa điểm C cách B là 72 km, thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút. Tính vận tốc thực của ca nô biết vận tốc dòng nước là 4km/h.
- A
36km/h
- B
30km/h
- C
40km/h
- D
38km/h
Đáp án : A
Các bước giải bài toán bằng cách lập phương trình:
+) Chọn ẩn và đặt điều kiện cho ẩn
+) Biểu thị các đại lượng chưa biết qua ẩn và các đại lượng đã biết.
+) Lập phương trình-giải phương trình.
+) Chọn kết quả và trả lời.

Phương trình: \(\dfrac{{72}}{{x - 4}} - \dfrac{{80}}{{x + 4}} = \dfrac{1}{4}\)
Gọi vận tốc thực của ca nô là \(x\left( {x > 0,km/h} \right)\)
Đổi 15 phút = \(\dfrac{{15}}{{60}} = \dfrac{1}{4}\)h
*) Xuôi dòng:
Vận tốc của ca nô là \(x + 4\left( {km/h} \right) \Rightarrow \) Thời gian xuôi dòng của ca nô là \(\dfrac{{80}}{{x + 4}}(h)\)
*) Ngược dòng:
Vận tốc ngược dòng của ca nô là \(x - 4\left( {km/h} \right) \Rightarrow \) Thời gian ngược dòng của ca nô là \(\dfrac{{72}}{{x - 4}}(h)\)
Vì thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút nên ta có phương trình:
\(\begin{array}{l}\;\;\;\;\dfrac{{72}}{{x - 4}} - \dfrac{{80}}{{x + 4}} = \dfrac{1}{4}\\ \Leftrightarrow \dfrac{{288(x + 4) - 320(x - 4)}}{{(x - 4)(x + 4)}} = \dfrac{{{x^2} - 16}}{{(x - 4)(x + 4)}}\\ \Rightarrow - 32x + 2432 = {x^2} - 16\\ \Leftrightarrow {x^2} + 32x - 2448 = 0\\\Delta = {16^2} + 2448 = 2704 \Rightarrow \sqrt \Delta = 52\end{array}\)
Phương trình có hai nghiệm \(x = - 16 + 52 = 36(tmdk)\),\(x = - 16 - 52 = - 68\) (loại)
Vậy vận tốc thực của ca nô là \(36km/h.\)
Lập phương trình bậc hai có hai nghiệm là \(\sqrt 5 - 2\) và \(\sqrt 5 + 2\).
- A
\({x^2} - 2\sqrt 5 \,x + 1 = 0\)
- B
\({x^2} - 3\sqrt 5 \,x + 2 = 0\)
- C
\({x^2} + 2\sqrt 5 \,x + 1 = 0\)
- D
\({x^2} - 3\sqrt 5 \,x - 2 = 0\)
Đáp án : A
\(\left\{ \begin{array}{l}u + v = S\\u.v = P\end{array} \right. \Rightarrow \) \(u,v\) là nghiệm của phương trình: \({x^2} - Sx + P = 0\). (ĐK: \({S^2} \ge 4P\) )
Ta có:
\(\begin{array}{l}S = \sqrt 5 - 2 + \sqrt 5 + 2 = 2\sqrt 5. \\P = (\sqrt 5 - 2)(\sqrt 5 + 2) = 5 - 4 = 1\end{array}\).
Nhận thấy \({S^2} > 4P\,\left( {{\rm{do}}\,{{\left( {2\sqrt 5 } \right)}^2} = 20 > 4} \right)\)
Nên phương trình bậc hai có 2 nghiệm \(\sqrt 5 - 2\) và \(\sqrt 5 + 2\) là: \({x^2} - 2\sqrt 5 \,x + 1 = 0\).
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O.\) Gọi $P,\,Q,R$ lần lượt là giao điểm của các tia phân giác trong góc \(A,\,B,\,C\) với đường tròn. Giả sử rằng \(S = AP \cap RQ.\) Khi đó:
- A
\(\widehat {ASQ} = {30^0}\)
- B
\(\widehat {ASQ} = {45^0}\)
- C
\(\widehat {ASQ} = {60^0}\)
- D
\(\widehat {ASQ} = {90^0}\)
Đáp án : D
- Sử dụng tính chất tia phân giác của một góc nội tiếp chia cung bị chắn thành hai cung bằng nhau.
- Tính chất góc có đỉnh nằm bên trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn.

Ta có tia phân giác \(AP\) chia đôi cung \(BC\) thành hai cung bằng nhau, hay\(sđ\overparen{BP} = sđ\overparen{CP}=\dfrac{1}{2}sđ\,\overparen{BC}.\)
Tương tự ta có $sđ\overparen{AQ} = sđ\overparen{CQ}=\dfrac{1}{2}sđ\,\overparen{AC} $$sđ\overparen{AR} = sđ\overparen{BR}=\dfrac{1}{2}sđ\,\overparen{AB} .$ Khi đó theo tính chất của góc có đỉnh bên trong đường tròn ta có
\(\begin{array}{l}\widehat {ASQ} = \dfrac{1}{2}\left( {sđ\,\overparen{AQ} + sđ\,\overparen{PR}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{1}{2}sđ\,\overparen{AC} + \dfrac{1}{2}sđ\,\overparen{AB} + \dfrac{1}{2}sđ\,\overparen{BC}} \right) \\= \dfrac{1}{2}\left( {\dfrac{1}{2}{{.360}^0}} \right) = {90^0}.\end{array}\)
Tính độ dài cạnh của tam giác đều nội tiếp \(\left( {O;R} \right)\) theo \(R.\)
- A
\(\dfrac{R}{{\sqrt 3 }}\)
- B
\(\sqrt 3 R\)
- C
\(R\sqrt 6 \)
- D
\(3R\)
Đáp án : B
+ Sử dụng tính chất tam giác đều để tìm bán kính đường tròn
+ Sử dụng định lý Pytago để tìm cạnh của tam giác đều
+ Sử dụng công thức tính diện tích tam giác \(S = \dfrac{{ah}}{2}\) với \(h\) là chiều cao ứng với cạnh đáy là \(a\) .

+ Gọi tam giác \(ABC\) đều cạnh \(a\) nội tiếp đường tròn \(\left( {O;R} \right)\) .
Khi đó \(O\) là trọng tâm tam giác \(ABC\) . Gọi \(AH\) là đường trung tuyến \( \Rightarrow R = AO = \dfrac{2}{3}AH \Rightarrow AH = \dfrac{{3R}}{2}\)
+ Theo định lý Pytago ta có \(A{H^2} = A{B^2} - B{H^2} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\)
Từ đó ta có \(\dfrac{{3R}}{2} = \dfrac{{a\sqrt 3 }}{2} \Rightarrow a = \sqrt 3 R\)
Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = mx + 1\). Gọi \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) là các giao điểm của \(\left( d \right)\) và \(\left( P \right)\). Tìm \(m\) để biểu thức \(M = \left( {{y_1} - 1} \right)\left( {{y_2} - 1} \right)\) đạt giá trị lớn nhất.
- A
\(m = 0\)
- B
\(m = 2\)
- C
\(m = 1\)
- D
\(m = - 1\)
Đáp án : A
+ Viết phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\).
+ Đánh giá \(M = \left( {{y_1} - 1} \right)\left( {{y_2} - 1} \right)\) bằng cách sử dụng hệ thức Vi-et.
Phương trình hoành độ giao điểm của đường thẳng và Parabol là: \({x^2} = mx + 1 \Leftrightarrow {x^2} - mx - 1 = 0\) (1)
\(\Delta = {m^2} + 4 > 0\) với mọi \(m\) nên (1) có hai nghiệm phân biệt, suy ra \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) với \({x_1};{x_2}\) là hai nghiệm của phương trình (1).
Theo định lý Viet, ta có: \({x_1} + {x_2} = m;{x_1}{x_2} = - 1\)
Vì \(A;B \in \left( P \right) \Rightarrow {y_1} = x_1^2;{y_2} = x_2^2\).
Ta có
$M = \left( {{y_1} - 1} \right)\left( {{y_2} - 1} \right) $$= \left( {x_1^2 - 1} \right)\left( {x_2^2 - 1} \right)$$ = x_1^2x_2^2 - \left( {x_1^2 + x_1^2} \right) + 1$
$ = x_1^2x_2^2 + 2{x_1}{x_2} - {\left( {{x_1} + {x_2}} \right)^2} + 1$ \( = 1 - 2 - {m^2} + 1 = - {m^2} \le 0\)
Vậy \(\max M = 0\) khi \(m = 0\).
Cho mặt cầu có thể tích \(V = 288\pi \,\left( {c{m^3}} \right)\) . Tính đường kính mặt cầu.
- A
\(6\,cm\)
- B
\(12\,cm\)
- C
\(8\,cm\)
- D
\(16\,cm\)
Đáp án : B
Sử dụng công thức thể tích khối cầu $V = \dfrac{4}{3}\pi {R^3}$ để tính bán kính, từ đó suy ra đường kính của mặt cầu.
Ta có \(V = \dfrac{4}{3}\pi {R^3} = 288\pi \Rightarrow {R^3} = 216 \Rightarrow R = 6\,cm\)
Từ đó đường kính mặt cầu là \(d = 2R = 2.6 = 12\,cm\).
Cho hình vẽ, tìm \(x.\)

- A
\(x = 0,75\)
- B
\(x = 4,5\)
- C
\(x = 4\sqrt 3 \)
- D
\(x = 4\)
Đáp án : B
Sử dụng hệ thức lượng trong tam giác vuông: “ bình phương cạnh góc vuông bằng tích hình chiếu của nó lên cạnh huyền với cạnh huyền”

Đặt tên như hình vẽ trên.
Tam giác \(MNP\) vuông tại \(M\) có \(MH \bot NP\)
Theo hệ thức lượng trong tam giác vuông ta có \(M{N^2} = N{H^2}.NP \Rightarrow {6^2} = x.8 \Rightarrow x = 36:8 = 4,5.\)
Vậy \(x = 4,5.\)
Tâm của đường tròn ngoại tiếp tam giác vuông là
- A
Trung điểm cạnh huyền
- B
Trung điểm cạnh góc vuông lớn hơn
- C
Giao ba đường cao
- D
Giao ba đường trung tuyến
Đáp án : A
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Cho tam giác $ABC$ nội tiếp đường tròn $\left( {O;R} \right)$ có $AB = 5cm,AC = 12cm$ và đường cao $AH = 3cm$ ($H$ nằm ngoài $BC$) , khi đó $R$ bằng
- A
$6cm$
- B
$6,5cm$
- C
$5cm$
- D
$7,5cm$
Đáp án : D
Dựa vào tính chất tứ giác nội tiếp
Định lí pi-ta-go
Dấu hiệu và tính chất hai tam giác đồng dạng

Vẽ đường kính $AD$.
Xét \(\Delta AHB\) vuông tại $H$ ta có $A{B^2} = A{H^2} + H{B^2}$ (Py-ta-go)
Mà $AB = 5cm,AH = 3cm$ nên $HB = 4cm$.
Ta có tứ giác $ABCD$ là tứ giác nội tiếp nên \(\widehat {ADC} + \widehat {ABC} = {180^0}\) (tính chất)
Lại có \(\widehat {ABC} + \widehat {ABH} = {180^0}\) (kề bù) nên \(\widehat {ADC} = \widehat {ABH}\).
Xét $\Delta AHB$ và \(\Delta DCA\) có:
\(\widehat {AHB} = \widehat {ACD} = {90^0}\)
\(\widehat {ADC} = \widehat {ABH}\) (cmt)
\( \Rightarrow \Delta AHB \backsim \Delta DCA\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{HB}}{{CA}} = \dfrac{{AB}}{{DA}} \Rightarrow DA = \dfrac{{CA.AB}}{{HB}} = \dfrac{{12.5}}{4} = 15 \Rightarrow OA = \dfrac{{15}}{2} = 7,5cm\)



