Bài 1.26 trang 16 SBT giải tích 12

Đề bài

Hàm số \(y = {\left( {x + 1} \right)^3}\left( {5 - x} \right)\) có mấy điểm cực trị?

A. \(0\)                         B. \(1\)

C. \(2\)                         D. \(3\)

Lời giải chi tiết

Ta có: \(y' = 3{\left( {x + 1} \right)^2}\left( {5 - x} \right) - {\left( {x + 1} \right)^3}\) \( = {\left( {x + 1} \right)^2}\left[ {3\left( {5 - x} \right) - x - 1} \right]\) \( = {\left( {x + 1} \right)^2}\left( {14 - 4x} \right)\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = \dfrac{7}{2}\end{array} \right.\)

Ta thấy \(x =  - 1\) là nghiệm bội hai nên \(y'\) không đổi dấu qua \(x =  - 1\); \(x = \dfrac{7}{2}\) là nghiệm đơn nên \(y'\) đổi dấu qua \(x = \dfrac{7}{2}\).

Vậy hàm số chỉ có \(1\) điểm cực trị.

Cách khác:

Có thể lập bảng biến thiên như sau:

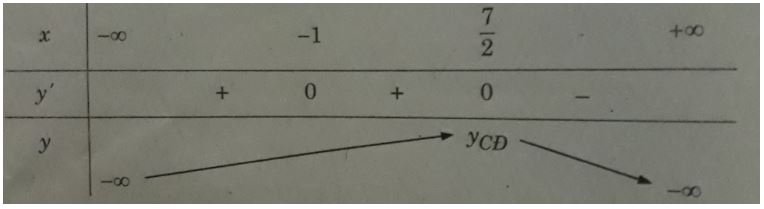
Chọn B.

[hoctot.me - Trợ lý học tập AI]