-
Exercise
-
QandA
-
Форумы
- Lớp 2
- Tự nhiên và xã hội
- Tiếng việt
- Toán học
- Tiếng Anh
- Đạo đức
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 4
- Khoa học
- Tiếng việt
- Toán học
- Đạo đức
- Tiếng Anh
- Lịch sử và Địa lí
- Công nghệ
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 5
- Khoa học
- Toán học
- Tiếng việt
- Tin học
- Tiếng Anh
- Đạo đức
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- Lớp 6
- Công nghệ
- Tin học
- Lịch sử và Địa lí
- GDCD
- Ngữ văn
- Toán học
- Khoa học tự nhiên
- Tiếng Anh
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 7
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Lịch sử và Địa lí
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Âm nhạc
- Lớp 8
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Ngữ văn
- Khoa học tự nhiên
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 9
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Lịch sử và Địa lí
- Lớp 10
- Hóa học
- Tiếng Anh
- Lịch sử
- Sinh học
- Địa lí
- Vật lí
- Tin học
- Toán học
- GD kinh tế và pháp luật
- Công nghệ
- Ngữ văn
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- GD Quốc phòng và An ninh
- Lớp 11
- Hóa học
- Tiếng Anh
- Vật lí
- Tin học
- Toán học
- Địa lí
- Công nghệ
- Lịch sử
- Ngữ văn
- Sinh học
- GD Thể chất
- GD Quốc phòng và An ninh
- GD kinh tế và pháp luật
- HĐ trải nghiệm, hướng nghiệp
-
Чат
-
Игры

- ИССЛЕДОВАТЬ
-
Exercise
-
QandA
-
Форумы
-
Tài liệu & đề thi
-
Ngữ pháp
-
Чат
- Статьи пользователей
- Игры
- FAVORITES
- Новости
- QandAs
- Toán Học
- Grade 8
- Cho tam giác ABC đồng dạng tam giác MPN. Gọi P, Q lần lượt là trung điểm của BC và PN a) Chứng minh tam giác ABP đồng dạng tam giác MPQ b) Chứng minh tam giác ACP đồng dạng tam giác MNQ c) Gọi G là trọng tâm của tam giác ABC,
Cho tam giác ABC đồng dạng tam giác MPN. Gọi P, Q lần lượt là trung điểm của BC và PN a) Chứng minh tam giác ABP đồng dạng tam giác MPQ b) Chứng minh tam giác ACP đồng dạng tam giác MNQ c) Gọi G là trọng tâm của tam giác ABC,
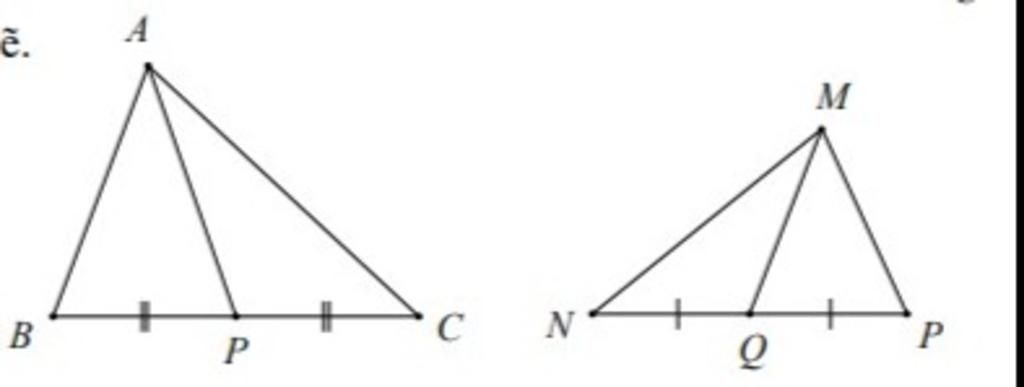
Cho tam giác ABC đồng dạng tam giác MPN. Gọi P, Q lần lượt là trung điểm của BC và PN
a) Chứng minh tam giác ABP đồng dạng tam giác MPQ
b) Chứng minh tam giác ACP đồng dạng tam giác MNQ
c) Gọi G là trọng tâm của tam giác ABC, K là trọng tâm của
tam giác MPN. Chứng minh tam giác ABG đồng dạng tam giác MPK
This anwser using AI, please
a) Để chứng minh tam giác ABP đồng dạng với tam giác MPQ, ta cần chứng minh tỉ lệ các cạnh tương ứng và góc tương ứng là bằng nhau.
- P là trung điểm của BC, nên BP = PC.
- Q là trung điểm của PN, nên PQ = QN.
- Tam giác ABC đồng dạng với tam giác MPN, nên có:
- Tỉ lệ cạnh:
\(\frac{AB}{MP} = \frac{AC}{MN} = \frac{BC}{PN}\).
- Vì BP = PC và PQ = QN, ta có:
\(\frac{AB}{MP} = \frac{ABP}{MPQ}\)
- Góc ABP = góc MPQ (chúng là góc tương ứng).
Từ đó, ta kết luận rằng tam giác ABP đồng dạng với tam giác MPQ.
b) Để chứng minh tam giác ACP đồng dạng với tam giác MNQ, ta cũng cần xét tỉ lệ cạnh và góc tương ứng.
- Tương tự như trên, ta có ACP với các cạnh tương ứng bằng một nửa:
- AC = MN (tương ứng với tỉ lệ đồng dạng đã nói ở trên).
- Góc ACP = góc MNQ.
Do đó, tam giác ACP đồng dạng với tam giác MNQ.
c) Gọi G là trọng tâm của tam giác ABC và K là trọng tâm của tam giác MPN. Trọng tâm G chia mỗi cạnh tương ứng theo tỉ lệ 2:1.
- Tỷ lệ cạnh cần cho tam giác ABG và MPK:
\(\frac{AG}{AB} = \frac{2}{3}\) và \(\frac{MK}{MP} = \frac{2}{3}\)
- Góc ABG = góc MPK (công thức tương ứng với góc trong các tam giác vừa hay).
Vì vậy, ta có tam giác ABG đồng dạng với tam giác MPK.
- P là trung điểm của BC, nên BP = PC.
- Q là trung điểm của PN, nên PQ = QN.
- Tam giác ABC đồng dạng với tam giác MPN, nên có:
- Tỉ lệ cạnh:
\(\frac{AB}{MP} = \frac{AC}{MN} = \frac{BC}{PN}\).
- Vì BP = PC và PQ = QN, ta có:
\(\frac{AB}{MP} = \frac{ABP}{MPQ}\)
- Góc ABP = góc MPQ (chúng là góc tương ứng).
Từ đó, ta kết luận rằng tam giác ABP đồng dạng với tam giác MPQ.
b) Để chứng minh tam giác ACP đồng dạng với tam giác MNQ, ta cũng cần xét tỉ lệ cạnh và góc tương ứng.
- Tương tự như trên, ta có ACP với các cạnh tương ứng bằng một nửa:
- AC = MN (tương ứng với tỉ lệ đồng dạng đã nói ở trên).
- Góc ACP = góc MNQ.
Do đó, tam giác ACP đồng dạng với tam giác MNQ.
c) Gọi G là trọng tâm của tam giác ABC và K là trọng tâm của tam giác MPN. Trọng tâm G chia mỗi cạnh tương ứng theo tỉ lệ 2:1.
- Tỷ lệ cạnh cần cho tam giác ABG và MPK:
\(\frac{AG}{AB} = \frac{2}{3}\) và \(\frac{MK}{MP} = \frac{2}{3}\)
- Góc ABG = góc MPK (công thức tương ứng với góc trong các tam giác vừa hay).
Vì vậy, ta có tam giác ABG đồng dạng với tam giác MPK.
Ответить
© 2025 Học Tốt Online - Chia Sẻ Tài Liệu Học Tập và Giải Bài Tập Miễn Phí  Russian
Russian