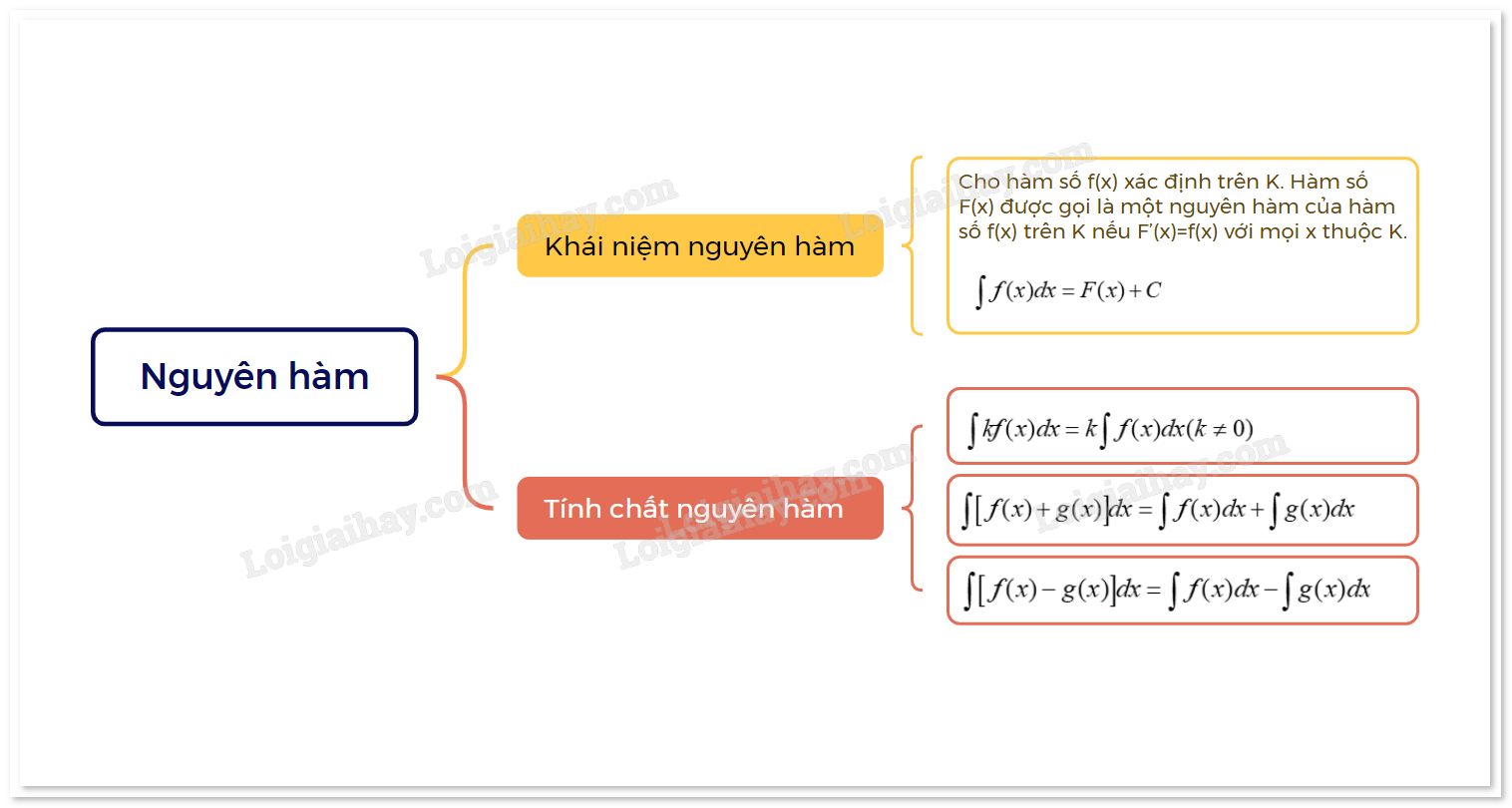
1. Khái niệm nguyên hàm
| Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x)=f(x) với mọi x thuộc K. |
Chú ý:
Cho K là một khoảng, đoạn hoặc nửa khoảng của tập số thực R
Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:
a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K
b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K
Họ (hay tập hợp) tất cả các nguyên hàm của hàm số f(x) trên K được kí hiệu là
\(\int {f(x)dx = F(x) + C} \)
2. Tính chất của nguyên hàm
|
English
Vietnamese
French
Russian