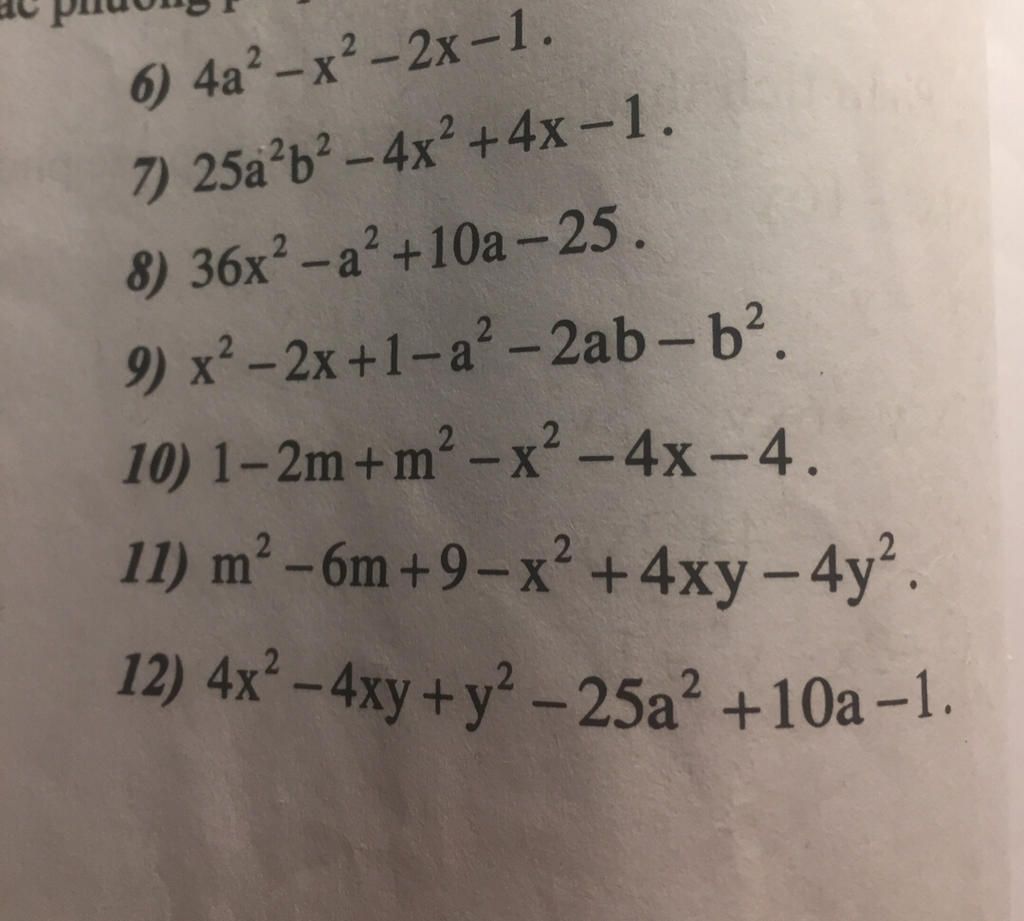Cứu emmmmmmmmmmmmmmmmmm
-
Exercise
-
QandA
-
Форумы
- Lớp 2
- Tự nhiên và xã hội
- Tiếng việt
- Toán học
- Tiếng Anh
- Đạo đức
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 4
- Khoa học
- Tiếng việt
- Toán học
- Đạo đức
- Tiếng Anh
- Lịch sử và Địa lí
- Công nghệ
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 5
- Khoa học
- Toán học
- Tiếng việt
- Tin học
- Tiếng Anh
- Đạo đức
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- Lớp 6
- Công nghệ
- Tin học
- Lịch sử và Địa lí
- GDCD
- Ngữ văn
- Toán học
- Khoa học tự nhiên
- Tiếng Anh
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 7
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Lịch sử và Địa lí
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Âm nhạc
- Lớp 8
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Ngữ văn
- Khoa học tự nhiên
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 9
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Lịch sử và Địa lí
- Lớp 10
- Hóa học
- Tiếng Anh
- Lịch sử
- Sinh học
- Địa lí
- Vật lí
- Tin học
- Toán học
- GD kinh tế và pháp luật
- Công nghệ
- Ngữ văn
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- GD Quốc phòng và An ninh
- Lớp 11
- Hóa học
- Tiếng Anh
- Vật lí
- Tin học
- Toán học
- Địa lí
- Công nghệ
- Lịch sử
- Ngữ văn
- Sinh học
- GD Thể chất
- GD Quốc phòng và An ninh
- GD kinh tế và pháp luật
- HĐ trải nghiệm, hướng nghiệp
-
Чат
-
Игры

- ИССЛЕДОВАТЬ
-
Exercise
-
QandA
-
Форумы
-
Tài liệu & đề thi
-
Ngữ pháp
-
Чат
- Статьи пользователей
- Игры
- FAVORITES
- Новости
Cứu emmmmmmmmmmmmmmmmmm
This anwser using AI, please
Để giải các phương trình này, chúng ta cần phân tích và biến đổi chúng thành dạng dễ giải hơn, thường là dạng phương trình bậc hai hoặc tìm nghiệm nếu có thể.
6) 4a² - x² - 2x - 1.
Chúng ta có thể sắp xếp lại để tìm nghiệm:
Khi đưa về dạng chuẩn, ta được x² + 2x + (1 - 4a²) = 0.
Dùng công thức nghiệm cho phương trình bậc hai: x = (-b ± √(b² - 4ac)) / 2a.
7) 25a²b² - 4x² + 4x - 1.
Biến đổi theo dạng bậc hai: -4x² + 4x + (25a²b² - 1) = 0.
Áp dụng công thức nghiệm cho x.
8) 36x² - a² + 10a - 25.
Sắp xếp lại: 36x² = a² - 10a + 25.
Giải phương trình này sẽ cho bạn kết quả cho x tùy thuộc vào a.
9) x² - 2x + 1 - a² - 2ab - b².
Sắp xếp lại: x² - 2x + (1 - a² - 2ab - b²) = 0.
Sử dụng công thức nghiệm bậc hai.
10) 1 - 2m + m² - x² - 4x - 4.
Đưa về dạng bậc hai sẽ có: m² - 2m + (1 - x² - 4x - 4) = 0.
Giải theo công thức nghiệm.
11) m² - 6m + 9 - x² + 4xy - 4y².
Dễ nhận thấy đây là một phương trình có thể phân tích hoặc đưa về bậc hai theo m.
12) 4x² - 4xy + y² - 25a² + 10a - 1.
Phân tích hoặc sắp xếp lại để giải cho y hoặc a.
Nhìn chung, việc giải từng phương trình bậc hai yêu cầu sắp xếp lại các hạng tử và sử dụng công thức nghiệm hoặc các phương pháp khác để tìm điều kiện tồn tại của nghiệm. Các phương trình này thường có hình dạng quen thuộc với các hạng tử bậc hai và do đó có thể áp dụng công thức nghiệm để tìm ra giá trị.
6) 4a² - x² - 2x - 1.
Chúng ta có thể sắp xếp lại để tìm nghiệm:
Khi đưa về dạng chuẩn, ta được x² + 2x + (1 - 4a²) = 0.
Dùng công thức nghiệm cho phương trình bậc hai: x = (-b ± √(b² - 4ac)) / 2a.
7) 25a²b² - 4x² + 4x - 1.
Biến đổi theo dạng bậc hai: -4x² + 4x + (25a²b² - 1) = 0.
Áp dụng công thức nghiệm cho x.
8) 36x² - a² + 10a - 25.
Sắp xếp lại: 36x² = a² - 10a + 25.
Giải phương trình này sẽ cho bạn kết quả cho x tùy thuộc vào a.
9) x² - 2x + 1 - a² - 2ab - b².
Sắp xếp lại: x² - 2x + (1 - a² - 2ab - b²) = 0.
Sử dụng công thức nghiệm bậc hai.
10) 1 - 2m + m² - x² - 4x - 4.
Đưa về dạng bậc hai sẽ có: m² - 2m + (1 - x² - 4x - 4) = 0.
Giải theo công thức nghiệm.
11) m² - 6m + 9 - x² + 4xy - 4y².
Dễ nhận thấy đây là một phương trình có thể phân tích hoặc đưa về bậc hai theo m.
12) 4x² - 4xy + y² - 25a² + 10a - 1.
Phân tích hoặc sắp xếp lại để giải cho y hoặc a.
Nhìn chung, việc giải từng phương trình bậc hai yêu cầu sắp xếp lại các hạng tử và sử dụng công thức nghiệm hoặc các phương pháp khác để tìm điều kiện tồn tại của nghiệm. Các phương trình này thường có hình dạng quen thuộc với các hạng tử bậc hai và do đó có thể áp dụng công thức nghiệm để tìm ra giá trị.
Ответить
© 2025 Học Tốt Online - Chia Sẻ Tài Liệu Học Tập và Giải Bài Tập Miễn Phí  Russian
Russian