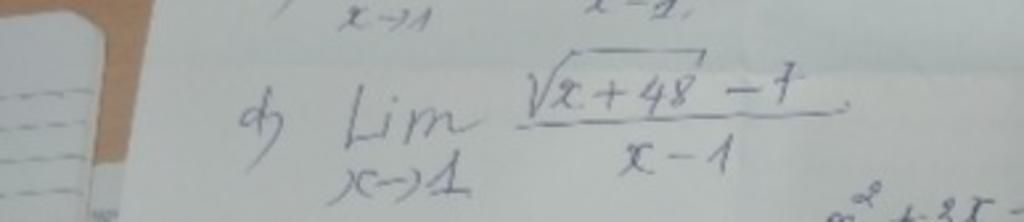-
Exercise
-
QandA
-
Forums
- Lớp 2
- Tự nhiên và xã hội
- Tiếng việt
- Toán học
- Tiếng Anh
- Đạo đức
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 4
- Khoa học
- Tiếng việt
- Toán học
- Đạo đức
- Tiếng Anh
- Lịch sử và Địa lí
- Công nghệ
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 5
- Khoa học
- Toán học
- Tiếng việt
- Tin học
- Tiếng Anh
- Đạo đức
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- Lớp 6
- Công nghệ
- Tin học
- Lịch sử và Địa lí
- GDCD
- Ngữ văn
- Toán học
- Khoa học tự nhiên
- Tiếng Anh
- Âm nhạc
- Mỹ thuật
- HĐ trải nghiệm, hướng nghiệp
- Lớp 7
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Lịch sử và Địa lí
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Âm nhạc
- Lớp 8
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Ngữ văn
- Khoa học tự nhiên
- Lịch sử và Địa lí
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- Âm nhạc
- Lớp 9
- Tiếng Anh
- GDCD
- Toán học
- Công nghệ
- Tin học
- Ngữ văn
- Khoa học tự nhiên
- HĐ trải nghiệm, hướng nghiệp
- Lịch sử và Địa lí
- Lớp 10
- Hóa học
- Tiếng Anh
- Lịch sử
- Sinh học
- Địa lí
- Vật lí
- Tin học
- Toán học
- GD kinh tế và pháp luật
- Công nghệ
- Ngữ văn
- HĐ trải nghiệm, hướng nghiệp
- GD Thể chất
- GD Quốc phòng và An ninh
- Lớp 11
- Hóa học
- Tiếng Anh
- Vật lí
- Tin học
- Toán học
- Địa lí
- Công nghệ
- Lịch sử
- Ngữ văn
- Sinh học
- GD Thể chất
- GD Quốc phòng và An ninh
- GD kinh tế và pháp luật
- HĐ trải nghiệm, hướng nghiệp
-
Discussion
-
Jeux

- EXPLORER
-
Exercise
-
QandA
-
Forums
-
Tài liệu & đề thi
-
Ngữ pháp
-
Discussion
- Blogs
- Jeux
- FAVORITES
- Fil d’actualités
Tính giới hạn của dãy số và hàm số
This anwser using AI, please
Để tính giới hạn của biểu thức sau:
Lim (x→1) (√(x + 48) - 7) / (x - 1)
Đầu tiên, chúng ta sẽ thay thế x = 1 vào biểu thức để kiểm tra giới hạn:
Khi x = 1, ta có:
√(1 + 48) - 7 = √49 - 7 = 7 - 7 = 0
và
x - 1 = 1 - 1 = 0.
Do đó, chúng ta có dạng 0/0, điều này cho thấy chúng ta cần áp dụng quy tắc L'Hôpital hoặc biến đổi đồng biến để giải quyết.
Bây giờ, chúng ta sẽ biến đổi biểu thức bằng cách nhân cả tử và mẫu với liên hợp của tử số:
(√(x + 48) - 7) * (√(x + 48) + 7) / (x - 1)(√(x + 48) + 7)
Khi nhân tử số, chúng ta sẽ có:
(√(x + 48))^2 - 7^2 = (x + 48) - 49 = x - 1.
Vì vậy, biểu thức trở thành:
(x - 1) / [(x - 1)(√(x + 48) + 7)]
Chúng ta có thể rút gọn (x - 1) ở tử và mẫu:
= 1 / (√(x + 48) + 7)
Bây giờ, chúng ta thay x = 1 vào biểu thức đã rút gọn:
= 1 / (√(1 + 48) + 7) = 1 / (√49 + 7) = 1 / (7 + 7) = 1 / 14.
Vậy giới hạn của dãy số và hàm số này là 1/14.
Lim (x→1) (√(x + 48) - 7) / (x - 1)
Đầu tiên, chúng ta sẽ thay thế x = 1 vào biểu thức để kiểm tra giới hạn:
Khi x = 1, ta có:
√(1 + 48) - 7 = √49 - 7 = 7 - 7 = 0
và
x - 1 = 1 - 1 = 0.
Do đó, chúng ta có dạng 0/0, điều này cho thấy chúng ta cần áp dụng quy tắc L'Hôpital hoặc biến đổi đồng biến để giải quyết.
Bây giờ, chúng ta sẽ biến đổi biểu thức bằng cách nhân cả tử và mẫu với liên hợp của tử số:
(√(x + 48) - 7) * (√(x + 48) + 7) / (x - 1)(√(x + 48) + 7)
Khi nhân tử số, chúng ta sẽ có:
(√(x + 48))^2 - 7^2 = (x + 48) - 49 = x - 1.
Vì vậy, biểu thức trở thành:
(x - 1) / [(x - 1)(√(x + 48) + 7)]
Chúng ta có thể rút gọn (x - 1) ở tử và mẫu:
= 1 / (√(x + 48) + 7)
Bây giờ, chúng ta thay x = 1 vào biểu thức đã rút gọn:
= 1 / (√(1 + 48) + 7) = 1 / (√49 + 7) = 1 / (7 + 7) = 1 / 14.
Vậy giới hạn của dãy số và hàm số này là 1/14.
Publier la réponse
© 2025 Học Tốt Online - Chia Sẻ Tài Liệu Học Tập và Giải Bài Tập Miễn Phí  French
French